
Over the past few weeks I've been making the paper geodesic icosahedron pictured above.
As with all my other balls in the past few months, I got the nets from Vince Matsko's website. The problem with this model is his instructions aren't very useful if you don't have Magnus Wenninger's Spherical Models book:
Not so challenging as its 8-frequency companion, this model requires just 320 individual spherical triangles of 5 distinct types. Bands are labelled numerically as in Figure 48 (p. 95) of Wenninger's Spherical Models. Although not individually labelled, the bands adhere to the following scheme: in Table 4, the arc in the third column of the list of bands is always next to the tab. You can easily check this by noting that in a circle, larger angles subtend larger chords, so you can measure chords to find out which angle is which.
The finished model will be approximately 14 inches (36 cm) in diameter.
Vince's net pdf document contains bands for the five different triangles. But without Wenninger's book, you've got no way to know which band is which. So here's one I prepared earlier:
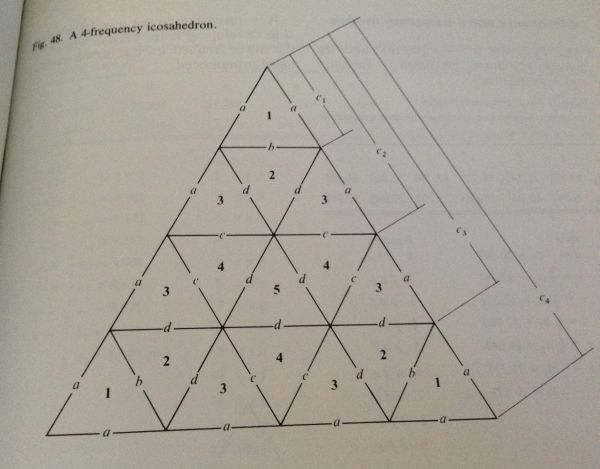
You can see from the diagram there are five different shaped triangles, numbered 1 to 5. This matches the pdf document on Vince Matsko's site. Also take note of the lettering - letters a to d indicate the length of each side (remember these aren't equilateral triangles! see Wenninger's book for more details on the mathematics of it).
The next line of instructions:
Although not individually labelled, the bands adhere to the following scheme: in Table 4, the arc in the third column of the list of bands is always next to the tab.
Again, without the book you've got no hope. And even if you do have the book, it can take a while to figure out what he actually means. Eventually I figured it out. Here's the table he's talking about:

Highlighted on the right is the "third column" he's talking about. If you look at the first picture from the book further up, you can see that triangle number 1 has "a", "a", and "b" as the lengths of its bands. And triangle 2 has "b", "d" and "d". And so on. The table above shows this as well. Now, in the table above, what he's saying is that the "tab" in the printouts is always next to the letter in the third column. So for triangle 1, in his pdf it will be a-b-a-tab. Triangle 2 will be d-b-d-tab, and so on. Here's what it will look like:

You'll note above that triangle 3 is asymmetric (look at the big triangle at the top to confirm this). Half the triangles are "left-handed" and half are "right-handed". If you were to print out all the copies of triangle 3 and fold them the same way it wouldn't work.
Here's the diagram from the book, but also showing the locations of the tabs once it's all put together, and showing left and right handed triangle 3.

Now the triangle above is just one "face" of an icosahedron. Remember an icosahedron has twenty sides. So you will need 60 bands for triangle 1, 60 for triangle 2, 120 for triangle 3 (60 left-handed and 60 right handed), 60 for triangle 4 and 20 for triangle 5. Using Vince Matsko's nets that's 10 pages for 1, 2 and 4, 20 pages of 3, and 3.3 pages of 5 (4 pages with a couple of leftovers).
But. If you were to print out the nets on A4 paper, the ball would be *huge* - double the size he says in his instructions. So I resized the images and pasted them into a word document. While I was at it, I flipped a copy of triangle 3 so the black lines would always be on the outside. Attached is my word doc with the nets that I used. It includes instructions on how many of each triangle you will need.
Right. So now we've got the design sorted, let's get started.
I printed each triangle on a different coloured piece of paper. And for triangle 3, I did the left and right handed triangles on different coloured paper (blue and green).

Next, cut them up. Each one took about thirty five seconds to cut.
Once they're cut, fold them up. I folded them so that the black line from the printout would always been on the outside. Each one took about twenty five seconds to fold. I did most of this in front of the tv.

Once they're glued into triangles (each one took about fifteen seconds), you can lay them out to see what they will look like before gluing.

I started a production line - got all sixteen little triangles for each face and put them together.


Then I put them together in the correct configuration, with all the tabs in the correct locations.

And then glued them all together. Here's all twenty faces glued:

Now for the really fun part - gluing all twenty faces together into a ball!



With six faces to go, it will fit quite nicely over your head.. ;)

And finally, we're finished!

A very time consuming, but quite impressive effort :)
Prabhakar
Absolutely outstanding!!
Well done you!